(通讯员:关迪)2023年12月20日14:00 ,北京大学光华管理学院涂云东教授为我院做线上学术报告,会议由学院副院长杨凯副教授主持,学院部分老师、研究生参加了本次线上学术报告会。
报告人简介:涂云东,北京大学光华管理学院和北京大学统计科学中心联席教授。国家级称号获得者,入选“日出东方”北大光华青年人才,北京大学优秀博士学位论文指导教师,2004年和2006年先后获武汉大学理学学士学位和经济学硕士学位,2012年获美国加州大学河滨分校经济学博士学位。亚太青年计量经济学者会议发起人和主要组织者。40余篇学术论文发表在多个国际国内知名专业杂志。著作教材《时间序列分析》由人民邮电出版社于2022年9月出版。主持多个国家自然科学基项目,并担任自然科学基金匿名评审。曾获世界计量经济学会、加州计量经济学会议等学术组织提供的青年学者研究资助。研究领域涵盖时间序列分析、非参数计量方法、大数据分析、金融计量和预测等。
报告题目:Regime-specific Return Predictability in Quantiles
摘要:This paper proposes a predictive quantile regression with multiple thresholds to capture the underlying regime switching mechanism in the prediction of stock returns. The predictability of each predictor is allowed to switch from one regime to another according to the value of a threshold variable and could vary across quantiles, and the predictors could possess different degrees of persistence. A sequential estimation procedure joint with an adaptive group Lasso refinement, is proposed to efficiently and consistently estimate the unknown multiple thresholds. To remove the impact of model misspecification from the sequential estimation on subsequent inference for the thresholds, a partitioned estimation of the thresholds is further considered. The resulting threshold estimators do not depend on parameters from other regimes asymptotically and have symmetric limiting distributions. The adaptive Lasso is finally adopted to identify the important predictors in each regime to improve prediction accuracy at each quantile. and is shown to achieve the oracle property Monte Carlo simulations demonstrate the nice performance of our procedure in finite samples. The empirical analysis for the U.S. stock returns shows that the return predictability changes with the economy policy uncertainty across the quantiles.


涂云东教授在本次研究中,提出了一种具有多阈值的分位数回归预测算法,以捕捉股票收益预测中潜在的区制转换机制。涂教授从平均回归预测开始讲起,详细了讲述了平均回归预测的理论和公式,然后引入分位数回归预测基础理论,并且详细解释了为什么收益的可预测性较弱等问题。
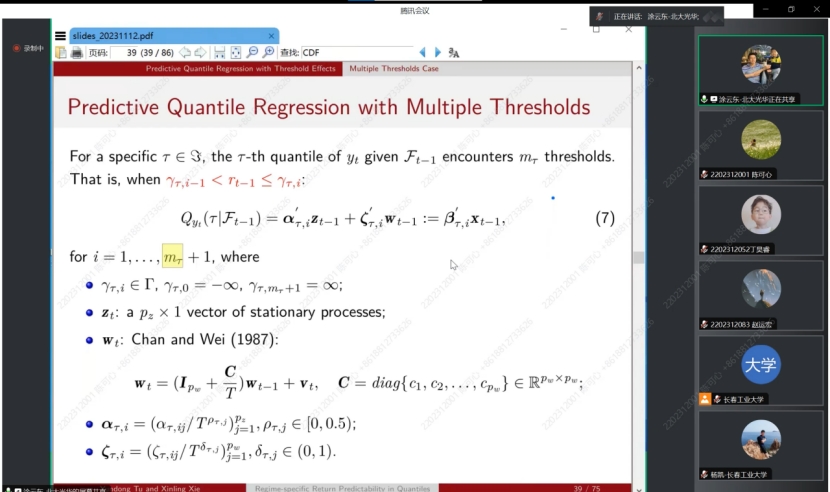
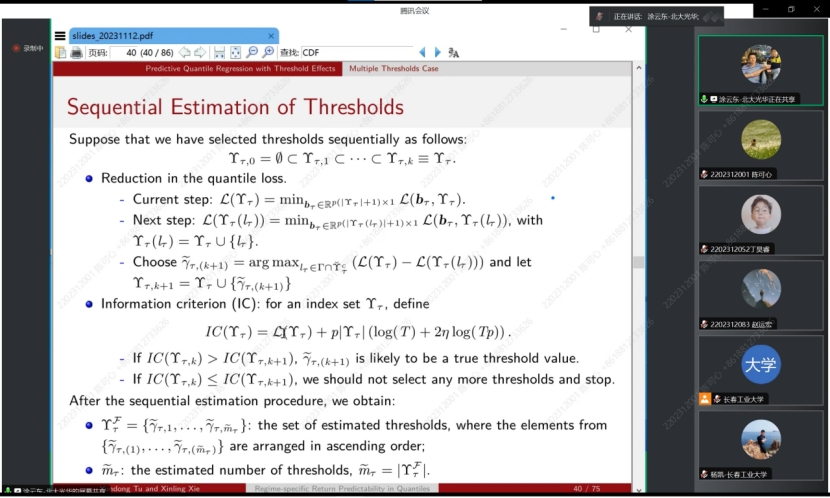
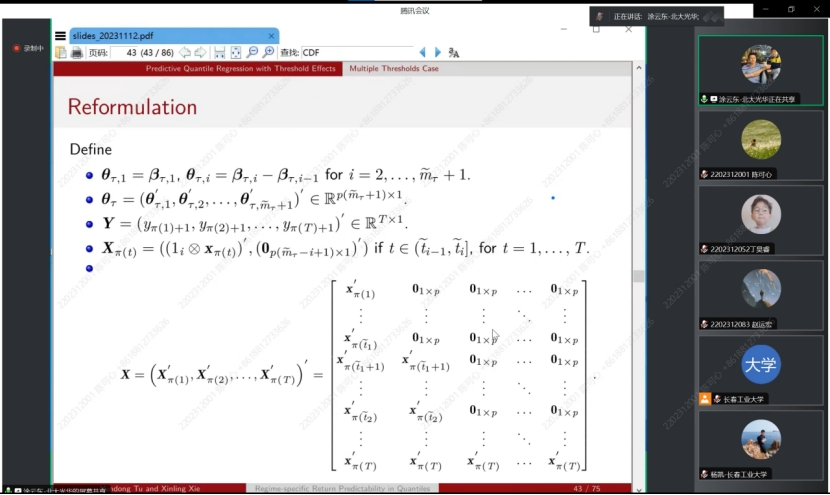
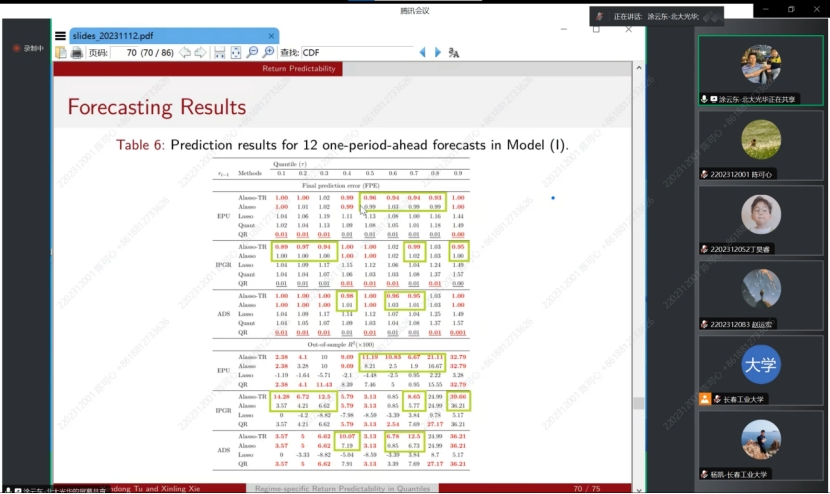
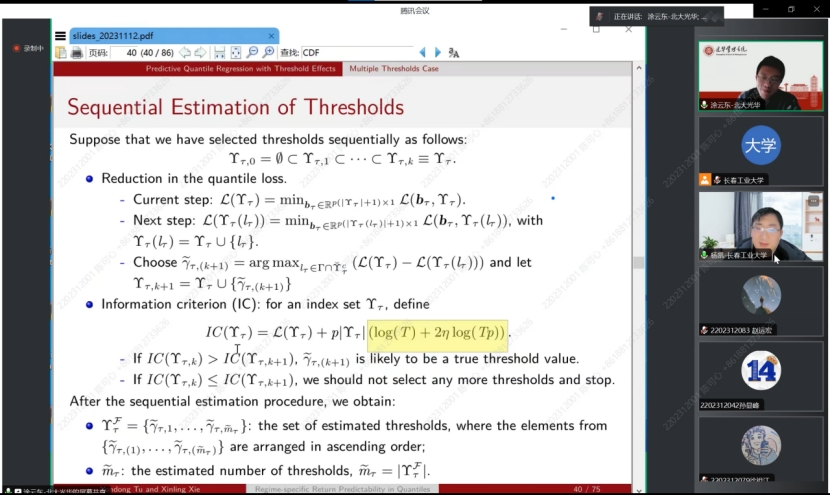
在接下来的讲解中,涂云东教授为我们介绍了分位数回归预测的性质,每个预测子的可预测性可以根据阈值变量的值从一种状态切换到另一种状态,并且可以在分位数之间变化,并且预测器可以具有不同程度的持久性。提出了一种与自适应群Lasso相结合的序列估计方法,以有效且一致地估计未知的多个阈值。为了消除序列估计中模型错误指定对阈值后续推断的影响,进一步考虑了阈值的分区估计。所得到的阈值估计量不渐近地依赖于来自其他状态的参数,并且具有对称的极限分布。最后采用自适应Lasso来识别每个方案中的重要预测因子,以提高每个分位数的预测精度。蒙特卡罗模拟证明了该方法在有限样本中的良好性能。对美国股票收益率的实证分析表明,收益率的可预测性随着经济政策不确定性的不同而变化。
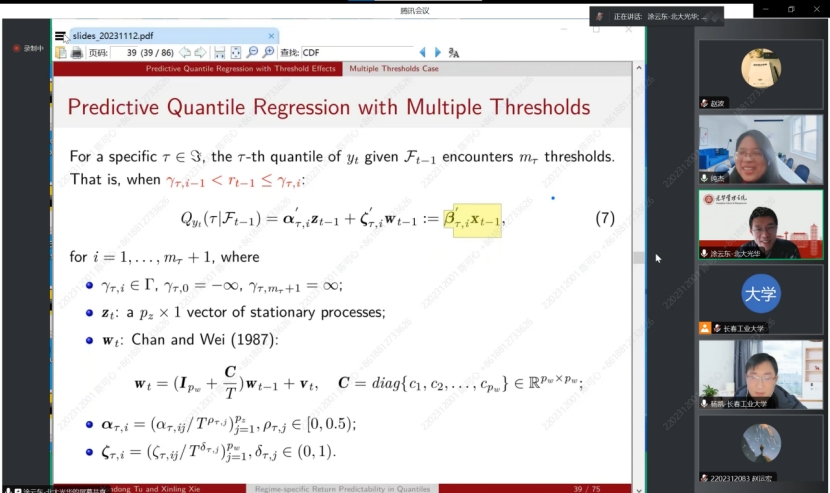
在会议的最后,各位老师和同学们就感兴趣的问题与涂教授进行了广泛的讨论和交流,教授们就提出的问题一一进行了详细的解答,使得在座的老师和同学收获颇丰。
本次学术交流会拓展了同学们的学术视野,也激发了同学们的学习热情,更加努力学习研究新的领域与方法,并使老师和同学们对分位数回归预测、自适应Lasso等方面有了更深的理解,聆听报告的师生均表示受益匪浅。
(审核人:王丹、王纯杰)
数学与统计学院
2023年12月20日